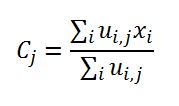الگوریتم خوشه بندی FCM
سه شنبه, ۱ فروردين ۱۳۹۶، ۰۲:۱۲ ب.ظ
در الگوریتم FCM، تعداد c مرکز (C1…Cc) در مجموعه به تصادف انتخاب میشود.
سپس درجه عضویت اعضا (xi) در هر خوشه تعیین (ui,j) و در مرحله بعد مراکز خوشه ها طبق رابطه زیر بروز میشوند و اینکار آنقدر ادامه خواهد داشت تا در مراکز کلاستر ها یا خوشه ها تغییر محسوسی صورت نگیرد (همگرایی):
این قسمت شامل تخمین موقعیت مراکز خوشه ها و تعریف قوانین فازی مرتبط با هر خوشه است. الگوریتم FCM مجموعه داده را با بهینه سازی یک تابع هدف، به زیر مجموعه های از پیش تعریف شده c پیکربندی میکند؛ که این زیر مجموعه ها نشان دهنده درجه مطلوبیت هر پارتیشن c خواهند بود. پیکربندی داده ها به خوشه ها، وابسته به شباهت یا عدم شباهت هر عضو خوشه است که معمولاً توسط محاسبه فاصله نقاط داده از مراکز خوشه ها بدست می آید.
معمولاً انتظار میرود که با افزایش تعداد مراکز خوشه ها دقت مدل نیز افزایش یابد. هرچند به جهت جلوگیری از رویداد بیش برازش مدل و هزینه های محاسباتی بیش از حد، پیشنهاد میشود که یافتن تعداد خوشه ها به صورت خودکار باشد.
برای این منظور شاخص های اعتبار و ارزیابی مختلفی پیشنهاد شده است. یکی از این توابع ارزیابی که در اجرا به خوبی عمل میکند توسط ژی و بنی (Xie and Beni) ارائه شده است. این تابع وابسته به واریانس کل از اندازه گیری مسافت هندسی و جداسازی مراکز خوشه ها است. تعداد بهینه مراکز خوشه ها را میتوان توسط فرآیندی تکرار پذیر بدست آورد.
سپس درجه عضویت اعضا (xi) در هر خوشه تعیین (ui,j) و در مرحله بعد مراکز خوشه ها طبق رابطه زیر بروز میشوند و اینکار آنقدر ادامه خواهد داشت تا در مراکز کلاستر ها یا خوشه ها تغییر محسوسی صورت نگیرد (همگرایی):
این قسمت شامل تخمین موقعیت مراکز خوشه ها و تعریف قوانین فازی مرتبط با هر خوشه است. الگوریتم FCM مجموعه داده را با بهینه سازی یک تابع هدف، به زیر مجموعه های از پیش تعریف شده c پیکربندی میکند؛ که این زیر مجموعه ها نشان دهنده درجه مطلوبیت هر پارتیشن c خواهند بود. پیکربندی داده ها به خوشه ها، وابسته به شباهت یا عدم شباهت هر عضو خوشه است که معمولاً توسط محاسبه فاصله نقاط داده از مراکز خوشه ها بدست می آید.
معمولاً انتظار میرود که با افزایش تعداد مراکز خوشه ها دقت مدل نیز افزایش یابد. هرچند به جهت جلوگیری از رویداد بیش برازش مدل و هزینه های محاسباتی بیش از حد، پیشنهاد میشود که یافتن تعداد خوشه ها به صورت خودکار باشد.
برای این منظور شاخص های اعتبار و ارزیابی مختلفی پیشنهاد شده است. یکی از این توابع ارزیابی که در اجرا به خوبی عمل میکند توسط ژی و بنی (Xie and Beni) ارائه شده است. این تابع وابسته به واریانس کل از اندازه گیری مسافت هندسی و جداسازی مراکز خوشه ها است. تعداد بهینه مراکز خوشه ها را میتوان توسط فرآیندی تکرار پذیر بدست آورد.
۹۶/۰۱/۰۱